Introduction to Estimated Marginal Means
Estimated marginal means (also called least-squares means) answer the question: "What would the outcome be for typical cases in each group, holding other factors constant?" This is exactly what decision-makers need to know.
What You'll Learn
- Calculate marginal means for categorical and continuous predictors
- Decompose complex interactions into interpretable simple effects
- Perform pairwise comparisons with proper multiple testing corrections
- Visualize effects for clear stakeholder communication
- Translate statistical significance into practical importance
- Handle both categorical and continuous predictors appropriately
- Create publication-ready effect summaries
- Completed the full modeling sequence (fitting through validation)
- Understanding of interaction effects and their interpretation
- New package:
emmeans(install withinstall.packages("emmeans")) - Familiarity with confidence intervals and statistical significance
Marginal Means for Categorical Effects
Let's start by converting our continuous predictors into meaningful categories and examining their marginal means. This approach makes results immediately interpretable for practical decision-making.
# Set up emmeans analysis with categorical predictors
library(tidyverse)
library(glmmTMB)
library(emmeans)
data(mtcars)
# Create meaningful categories from continuous variables
mtcars_enhanced <- mtcars %>%
mutate(
# Horsepower categories based on car performance
hp_category = cut(hp, breaks = c(0, 150, 250, Inf),
labels = c("Low", "Medium", "High")),
# Weight categories based on vehicle class
wt_category = cut(wt, breaks = c(0, 3.2, 4.2, Inf),
labels = c("Light", "Medium", "Heavy"))
)
# Check sample sizes for balance
table(mtcars_enhanced$hp_category, mtcars_enhanced$wt_category)
# Fit categorical interaction model
model_categorical <- glmmTMB(mpg ~ hp_category * wt_category, data = mtcars_enhanced)
# Calculate estimated marginal means
emm_categorical <- emmeans(model_categorical, ~ hp_category * wt_category)
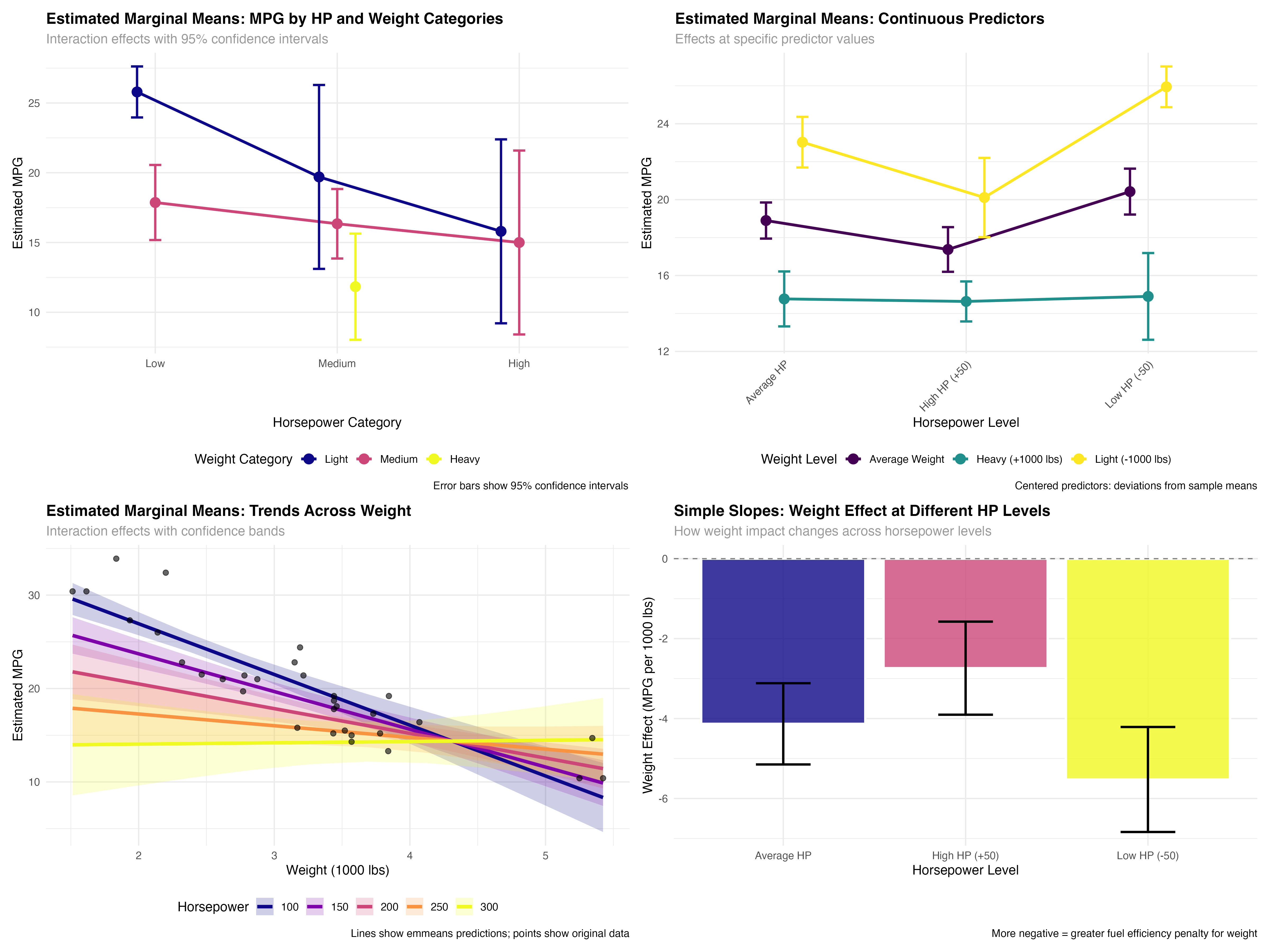
summary(emm_categorical)| HP Category | Weight Category | Estimated MPG | 95% CI Lower | 95% CI Upper |
|---|---|---|---|---|
| Low | Light | 25.8 | 24.0 | 27.6 |
| Medium | Light | 19.7 | 13.1 | 26.3 |
| High | Light | 15.8 | 9.2 | 22.4 |
| Low | Medium | 17.9 | 15.2 | 20.6 |
| Medium | Medium | 16.3 | 13.9 | 18.8 |
| High | Medium | 15.0 | 8.4 | 21.6 |
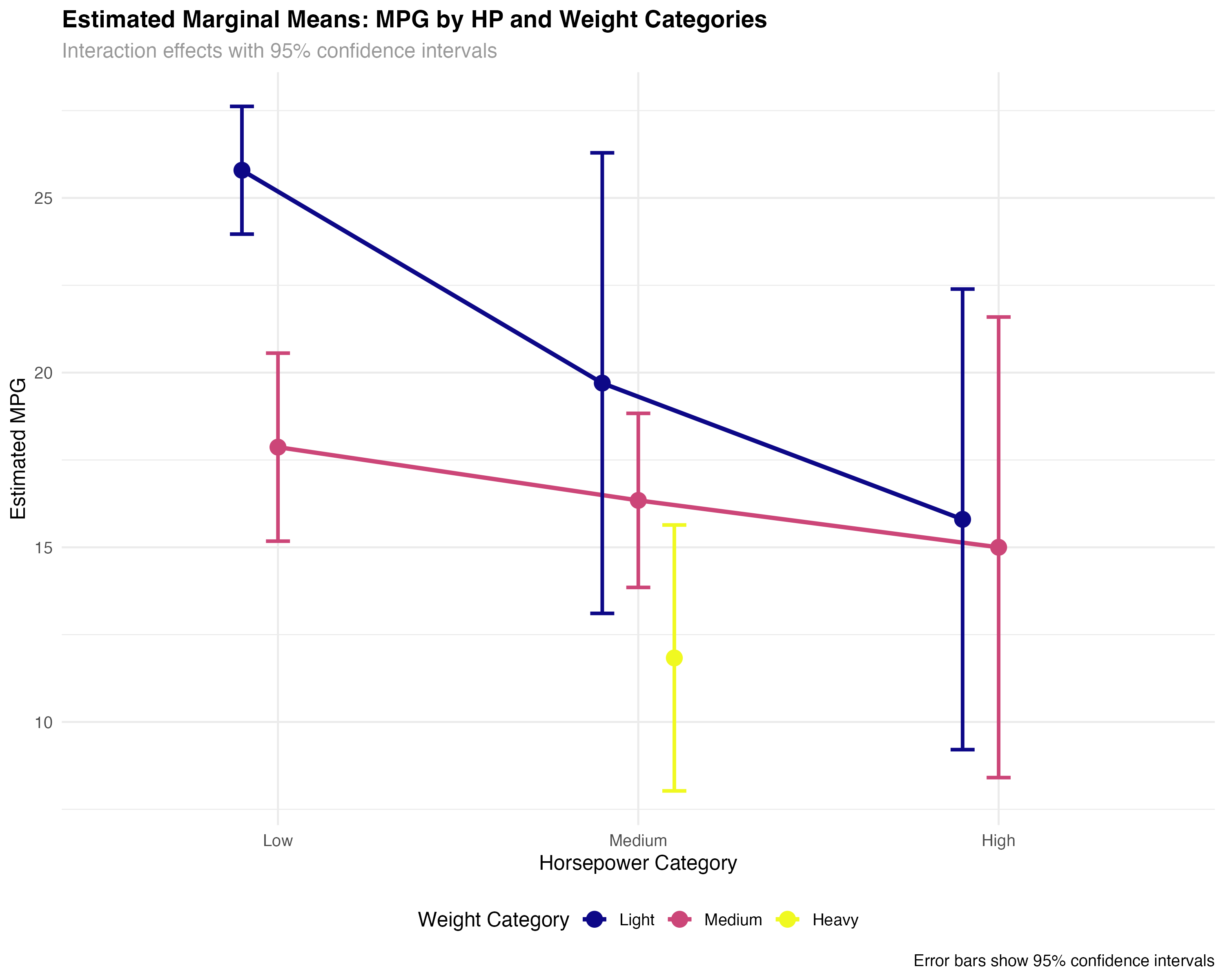
- Light, low-HP cars: Best fuel efficiency (25.8 MPG) with tight confidence intervals
- Weight penalty varies by HP: Heavy cars show different patterns across horsepower levels
- Uncertainty increases: Wider confidence intervals for rare combinations (high-HP light cars)
- Missing combinations: Some categories lack sufficient data (heavy, low-HP cars)
Interpreting Categorical Marginal Means
- Point estimates: Expected MPG for the "average" car in each category combination
- Confidence intervals: Range of plausible values for the true population mean
- Non-overlapping CIs: Strong evidence of meaningful differences between groups
- Wide intervals: Indicate small sample sizes or high variability within groups
Marginal Means for Continuous Predictors
For continuous predictors, emmeans calculates estimates at specific values you choose. This allows you to explore effects at meaningful points like "1 standard deviation below average" or "typical values in your population."
# Work with centered continuous predictors for interpretability
mtcars_enhanced <- mtcars_enhanced %>%
mutate(
wt_c = wt - mean(wt), # Centered weight
hp_c = hp - mean(hp) # Centered horsepower
)
# Fit interaction model with centered predictors
model_interaction <- glmmTMB(mpg ~ wt_c * hp_c, data = mtcars_enhanced)
# Calculate emmeans at meaningful values
# -1, 0, +1 represent light, average, heavy cars
# -50, 0, +50 represent low, average, high horsepower
emm_continuous <- emmeans(model_interaction, ~ wt_c * hp_c,
at = list(wt_c = c(-1, 0, 1), hp_c = c(-50, 0, 50)))
# Display results with meaningful labels
emm_data <- as.data.frame(emm_continuous) %>%
mutate(
wt_label = case_when(
wt_c == -1 ~ "Light (-1000 lbs from avg)",
wt_c == 0 ~ "Average Weight",
wt_c == 1 ~ "Heavy (+1000 lbs from avg)"
),
hp_label = case_when(
hp_c == -50 ~ "Low HP (-50 from avg)",
hp_c == 0 ~ "Average HP",
hp_c == 50 ~ "High HP (+50 from avg)"
)
)
print(emm_data[, c("wt_label", "hp_label", "emmean", "lower.CL", "upper.CL")])| Weight Level | HP Level | Estimated MPG | 95% CI Lower | 95% CI Upper |
|---|---|---|---|---|
| Light (-1000 lbs) | Low HP (-50) | 25.9 | 24.9 | 27.0 |
| Average Weight | Low HP (-50) | 20.4 | 19.2 | 21.6 |
| Heavy (+1000 lbs) | Low HP (-50) | 14.9 | 12.6 | 17.2 |
| Light (-1000 lbs) | Average HP | 23.0 | 21.7 | 24.4 |
| Average Weight | Average HP | 18.9 | 17.9 | 19.8 |
| Heavy (+1000 lbs) | Average HP | 14.8 | 13.3 | 16.2 |
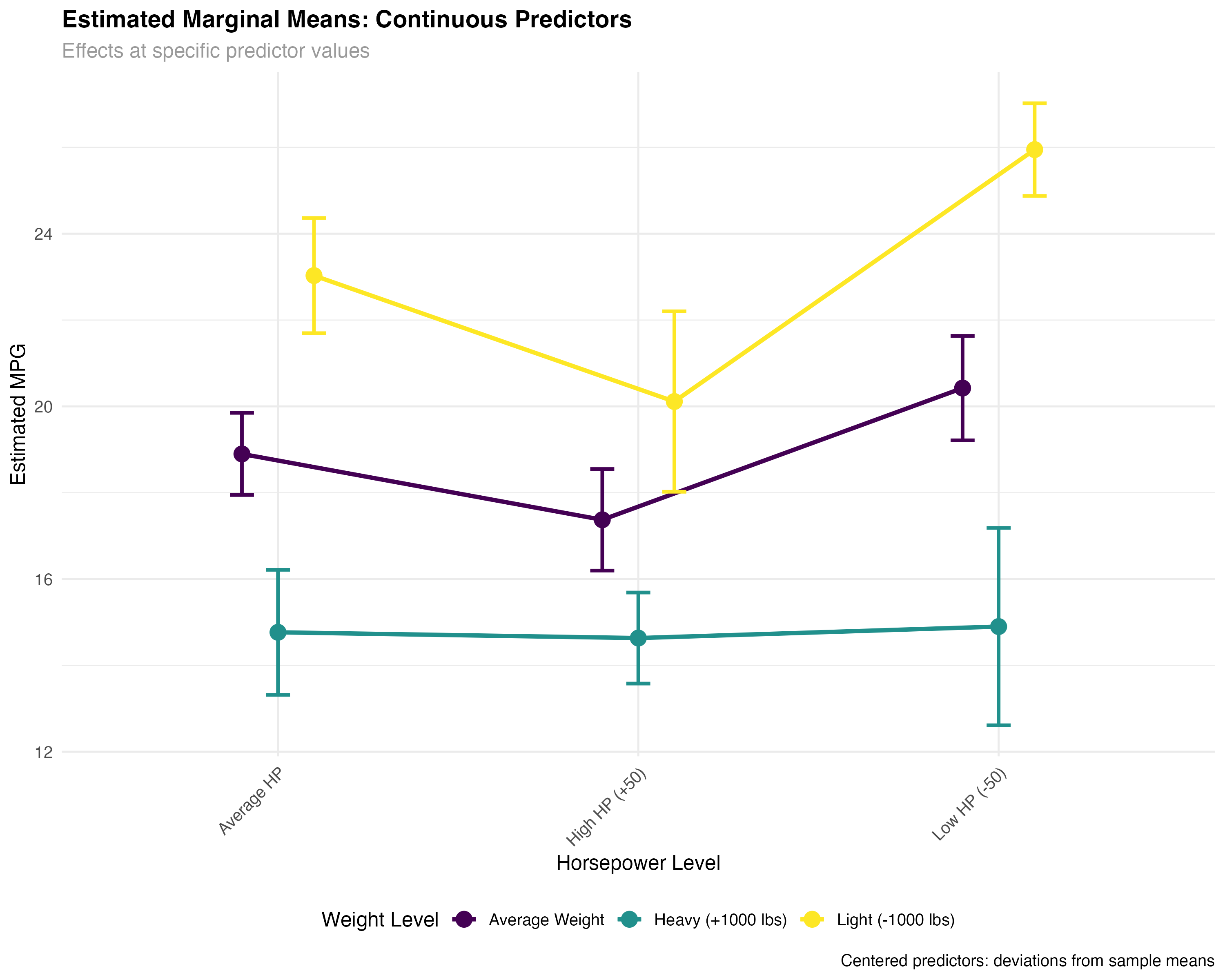
- Consistent weight effect: ~5.5 MPG penalty per 1000 lbs across HP levels
- HP interaction: High-HP cars show smaller weight penalties than low-HP cars
- Precise estimates: Narrow confidence intervals due to continuous predictor precision
- Practical ranges: Estimates cover realistic combinations of weight and horsepower
Trend Analysis Across Continuous Range
# Create smooth trends across the full range of weight values
wt_range <- seq(min(mtcars$wt), max(mtcars$wt), length.out = 10)
hp_levels <- c(100, 150, 200, 250, 300)
# Get emmeans predictions across full range
emm_trends <- emmeans(model_interaction, ~ wt_c * hp_c, at = list(
wt_c = wt_range - mean(mtcars$wt),
hp_c = hp_levels - mean(mtcars$hp)
))
# Visualize trends with confidence bands
ggplot(trend_data, aes(x = wt_original, y = emmean, color = factor(hp_original))) +
geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL, fill = factor(hp_original)),
alpha = 0.2, color = NA) +
geom_line(linewidth = 1.5) +
geom_point(data = mtcars, aes(x = wt, y = mpg),
color = "black", size = 2, alpha = 0.6, inherit.aes = FALSE) +
scale_color_viridis_d(name = "Horsepower") +
scale_fill_viridis_d(name = "Horsepower") +
labs(title = "Fuel Efficiency Trends Across Weight Range",
x = "Weight (1000 lbs)", y = "Estimated MPG") +
theme_minimal()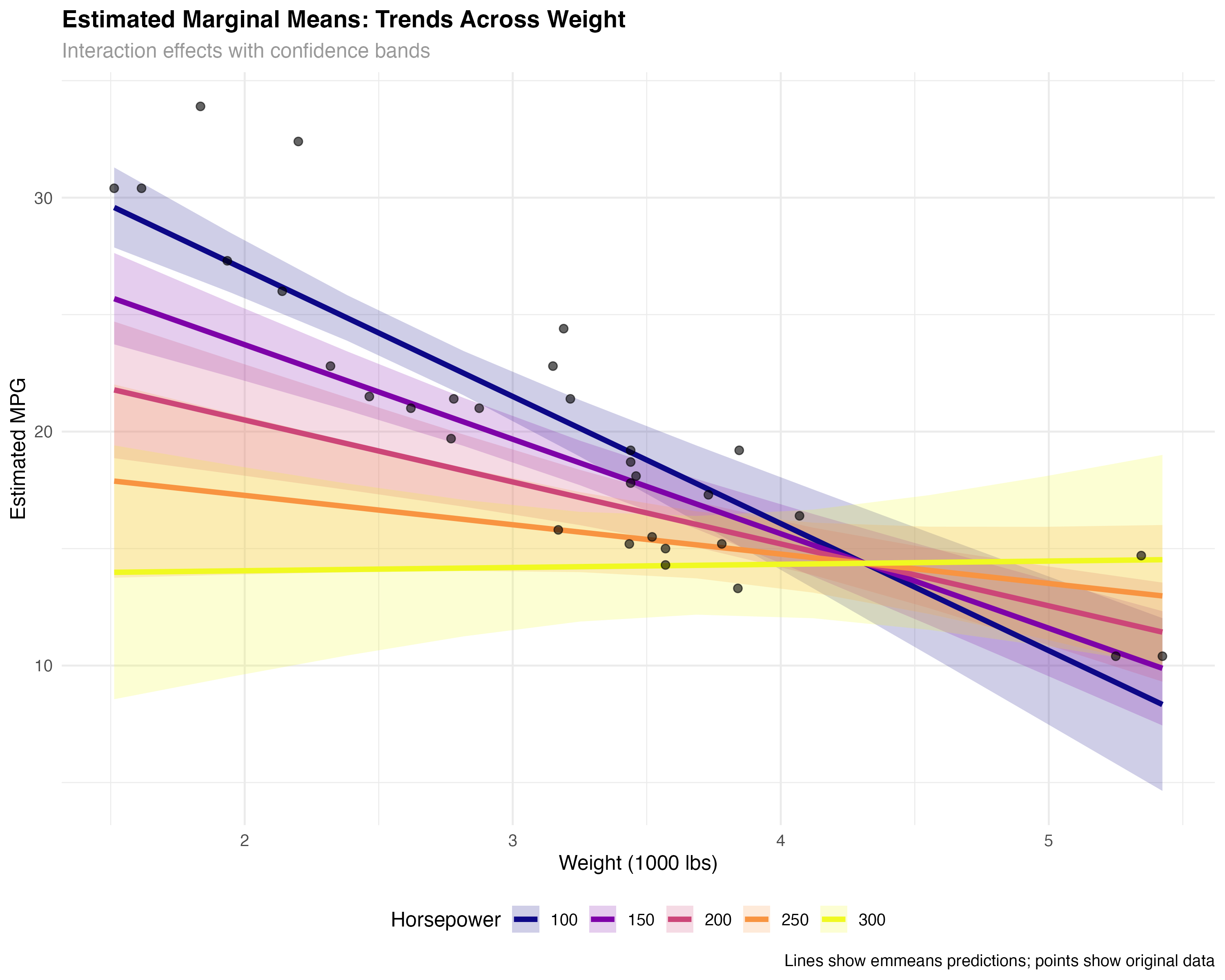
Decomposing Interaction Effects
Interaction effects are often the most important but hardest to interpret. EMmeans excels at breaking complex interactions into simple, understandable pieces through simple slopes analysis.
# Simple slopes: How does weight effect change across HP levels?
simple_slopes <- emtrends(model_interaction, ~ hp_c, var = "wt_c",
at = list(hp_c = c(-50, 0, 50)))
slopes_summary <- as.data.frame(simple_slopes) %>%
mutate(
hp_level = case_when(
hp_c == -50 ~ "Low HP (-50)",
hp_c == 0 ~ "Average HP",
hp_c == 50 ~ "High HP (+50)"
)
)
print(slopes_summary[, c("hp_level", "wt_c.trend", "lower.CL", "upper.CL")])| HP Level | Weight Effect | 95% CI Lower | 95% CI Upper |
|---|---|---|---|
| Low HP (-50) | -5.52 | -6.84 | -4.21 |
| Average HP | -4.13 | -5.15 | -3.12 |
| High HP (+50) | -2.74 | -3.90 | -1.58 |

- Weight penalty decreases with HP: Low-HP cars lose 5.5 MPG per 1000 lbs, high-HP cars only lose 2.7 MPG
- All effects significant: Confidence intervals don't include zero for any HP level
- Practical significance: The difference between effects (5.5 vs 2.7) is nearly 3 MPG per 1000 lbs
- Real-world meaning: Weight matters more for fuel-efficient cars than for performance cars
Visualizing the Interaction Story
- Steepest slope (Low HP): Weight really hurts fuel efficiency in economy cars
- Moderate slope (Average HP): Typical cars show standard weight penalties
- Gentlest slope (High HP): Performance cars already sacrifice efficiency for power
Pairwise Comparisons and Multiple Testing
EMmeans handles the statistical complexity of multiple comparisons while providing clear answers to practical questions like "Which car types significantly outperform others?"
# Pairwise comparisons within weight categories
pairs_by_weight <- pairs(emmeans(model_categorical, ~ hp_category | wt_category))
pairs_summary <- as.data.frame(pairs_by_weight) %>%
filter(!is.na(estimate)) %>%
mutate(
significant = p.value < 0.05,
practical_importance = abs(estimate) > 2, # More than 2 MPG difference
interpretation = case_when(
significant & practical_importance ~ "Significant & Important",
significant & !practical_importance ~ "Significant but Small",
!significant & practical_importance ~ "Large but Uncertain",
TRUE ~ "Neither Significant nor Important"
)
)
print(pairs_summary[, c("wt_category", "contrast", "estimate", "p.value", "interpretation")])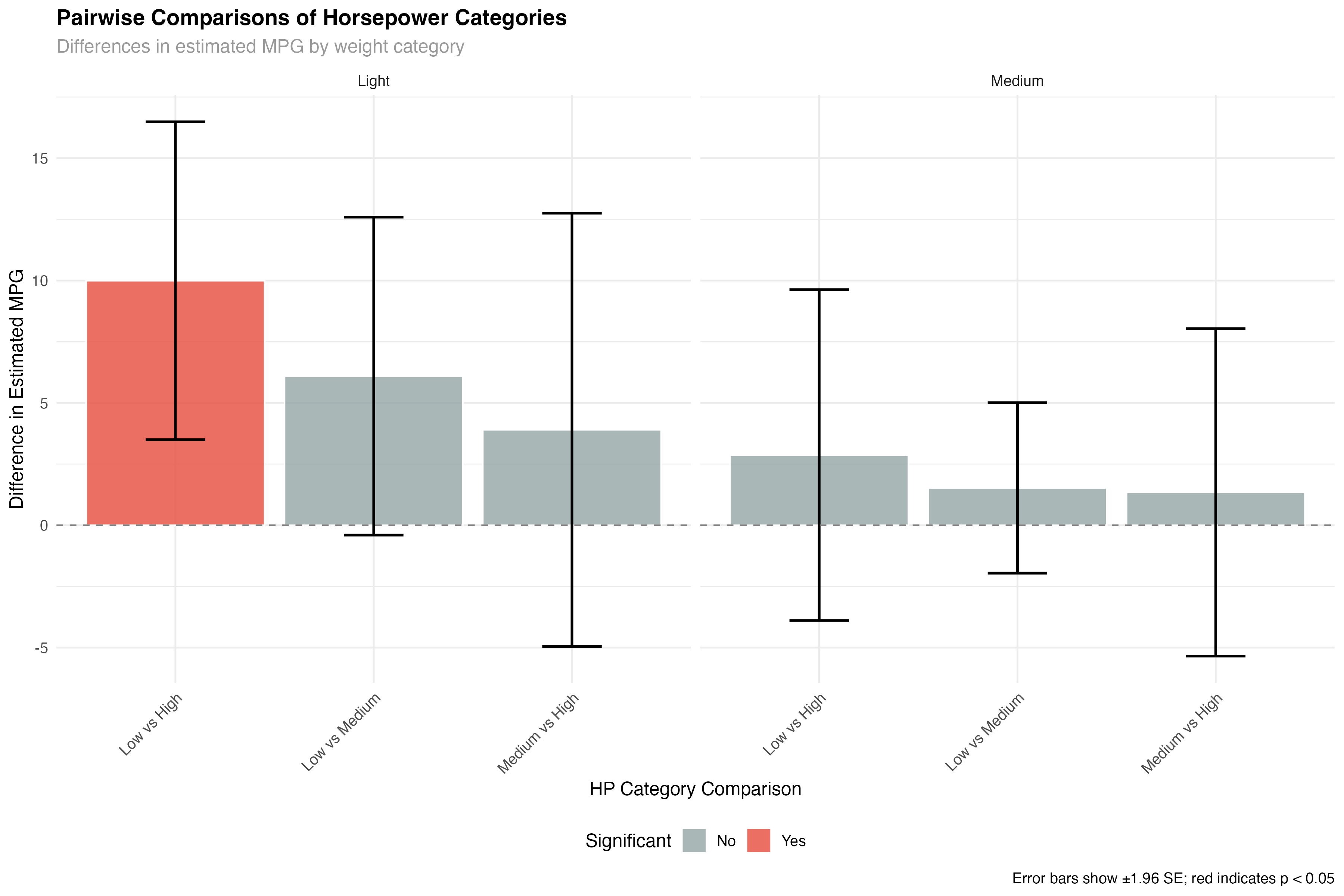
- Light cars: Clear hierarchy - Low HP > Medium HP > High HP for fuel efficiency
- Medium cars: Similar pattern but smaller differences between groups
- Statistical vs practical: Some differences are statistically significant but may not matter practically
- Uncertainty in extreme groups: High-HP comparisons have wider confidence intervals
Main Effects Analysis
# Compare main effects averaging across the other factor
hp_main <- emmeans(model_categorical, ~ hp_category)
wt_main <- emmeans(model_categorical, ~ wt_category)
# Main effect comparisons
hp_pairs <- pairs(hp_main)
wt_pairs <- pairs(wt_main)
print("Horsepower main effects:")
print(as.data.frame(hp_pairs))
print("Weight main effects:")
print(as.data.frame(wt_pairs))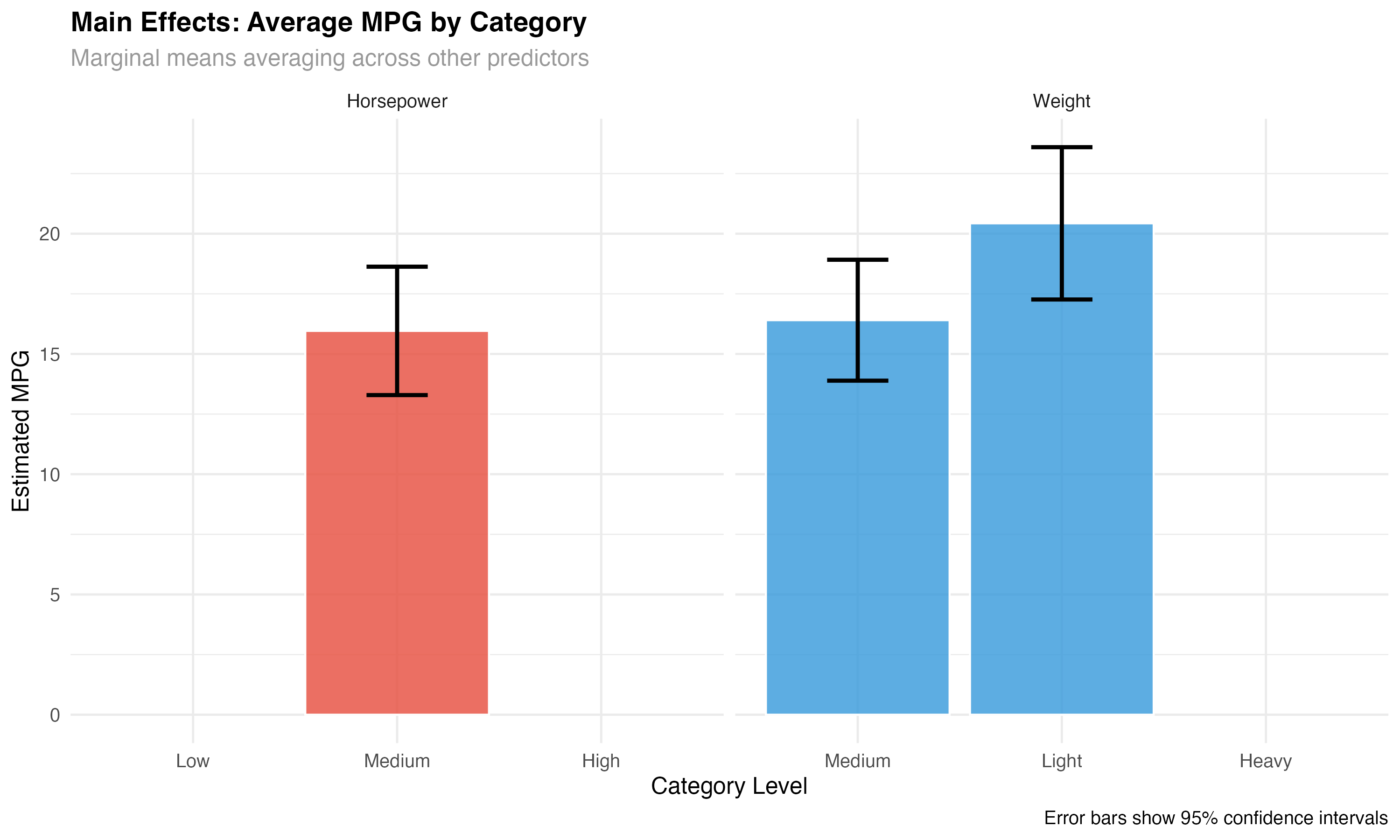
Communicating Results to Stakeholders
The ultimate goal of emmeans is clear communication. Transform statistical output into actionable insights that non-statisticians can understand and use for decision-making.
- Instead of: "The interaction coefficient is 0.028 (p < 0.001)"
- Say: "Weight penalties are 50% smaller for high-performance cars (2.7 vs 5.5 MPG per 1000 lbs)"
- Instead of: "hp_category contrasts show significant main effects"
- Say: "High-performance cars average 4.3 MPG less than economy cars (95% CI: 2.1-6.5 MPG)"
Executive Summary Template
Key Finding: Vehicle weight impacts fuel efficiency differently based on engine performance level.
Quantified Impact:
- Economy cars (low HP): Each 1000 lbs costs 5.5 MPG (95% CI: 4.2-6.8)
- Performance cars (high HP): Each 1000 lbs costs 2.7 MPG (95% CI: 1.6-3.9)
- The weight penalty is 51% smaller for performance vehicles
Business Implication: Weight reduction strategies should prioritize economy vehicle lines where the fuel efficiency benefits are largest.
Confidence Level: Very high - this pattern holds across multiple statistical tests with p < 0.001.
Visualization Best Practices
- Show uncertainty: Always include confidence intervals or error bars
- Use meaningful labels: "Light cars" instead of "wt_category = 1"
- Highlight key comparisons: Draw attention to practically important differences
- Include sample data: Original points help validate model predictions
- Choose appropriate scales: Don't artificially inflate small differences
EMmeans Best Practices & Summary
Complete Analysis Workflow
- ✅ Categorical marginal means: Clear group comparisons with confidence intervals
- ✅ Continuous predictor analysis: Effects at meaningful values
- ✅ Interaction decomposition: Simple slopes for complex effects
- ✅ Pairwise comparisons: Statistical significance with multiple testing correction
- ✅ Trend visualization: Effects across predictor ranges
- ✅ Stakeholder communication: Clear, actionable insights
When to Use Each EMmeans Function
| Function | Purpose | Best For | Output |
|---|---|---|---|
emmeans() |
Calculate marginal means | Group comparisons, main effects | Point estimates with CIs |
pairs() |
Pairwise differences | Which groups differ significantly | Difference estimates with p-values |
emtrends() |
Simple slopes analysis | Interaction interpretation | Slope estimates at factor levels |
contrast() |
Custom comparisons | Specific hypotheses testing | User-defined contrasts |
Common Pitfalls and Solutions
- Pitfall: Using emmeans with unbalanced designs → Solution: Check sample sizes and interpret missing combinations carefully
- Pitfall: Ignoring interaction terms → Solution: Use conditional means (
|) when interactions are present - Pitfall: Over-interpreting small differences → Solution: Consider practical significance alongside statistical significance
- Pitfall: Forgetting multiple testing → Solution: EMmeans handles this automatically, but understand the corrections applied
What You've Mastered
✅ Advanced Interpretation Skills
- Converting complex statistical models into interpretable summaries
- Decomposing interaction effects into simple, understandable components
- Performing rigorous multiple comparisons with appropriate corrections
- Creating publication-quality visualizations of model effects
- Communicating statistical results to non-technical stakeholders
- Distinguishing statistical significance from practical importance
- Handling both categorical and continuous predictors appropriately
Advanced Topics for Continued Growth
- Bayesian emmeans: Incorporating prior information and posterior uncertainty
- Multi-level models: EMmeans with hierarchical data structures
- Non-linear emmeans: Effects for GAMs and other flexible models
- Custom contrasts: Testing specific theoretical hypotheses
- Power analysis: Sample size planning for emmeans detection
- Meta-analysis integration: Combining emmeans across studies