🎯 Learning Objectives: Mastering Covariance Structures
📊 Case Study: Antidepressant Trial with Multiple Covariance Structures
A longitudinal RCT comparing three antidepressant treatments over 12 weeks, demonstrating how covariance structure assumptions impact clinical conclusions
Understanding Covariance Structures
Mathematical foundations and clinical implications
📐 Core Covariance Structure Concepts
library(tidyverse)
library(glmmTMB)
library(broom)
library(broom.mixed)
library(emmeans)
# Study parameters
n_patients <- 150
n_timepoints <- 6 # Baseline through Week 12
treatment_groups <- c("Placebo", "Low_Dose", "High_Dose")
# Create realistic patient demographics
patients <- tibble(
patient_id = 1:n_patients,
age = round(rnorm(n_patients, mean = 42, sd = 12)),
sex = sample(c("Female", "Male"), n_patients, replace = TRUE, prob = c(0.65, 0.35)),
baseline_severity = sample(c("Moderate", "Severe"), n_patients, replace = TRUE, prob = c(0.7, 0.3)),
baseline_hamd = round(pmax(14, rnorm(n_patients, mean = 22, sd = 4))),
treatment = rep(treatment_groups, length.out = n_patients) %>% sample(),
# Individual variation parameters for realistic covariance
patient_intercept = rnorm(n_patients, 0, 2.5),
patient_slope = rnorm(n_patients, 0, 0.8),
measurement_error_sd = rgamma(n_patients, shape = 2, rate = 4)
)
# Generate different covariance patterns for comparison
# Each pattern reflects different assumptions about temporal correlation- Constant variance across time
- Equal correlation between all pairs
- Lowest parameter count (2 parameters)
- Often violates exchangeability assumption
- Best for stable, repeated measurements
- Exponentially declining correlation
- Adjacent times most correlated
- Parsimonious (3 parameters)
- Natural for many biological processes
- Good for gradually changing outcomes
- Unique variance for each time point
- Unique correlation for each pair
- Maximum flexibility (21 parameters)
- Risk of overparameterization
- Best when pattern unknown
- Time-separation dependent correlation
- Allows heterogeneous variances
- Moderate parameter count (11 parameters)
- Flexible but structured
- Good compromise solution
Treatment Effect Comparison
How covariance assumptions impact efficacy estimation
# Fit models with different covariance assumptions
# 1. Compound Symmetry (Random Intercept)
model_cs <- glmmTMB(
hamd_score ~ treatment * week_scaled + baseline_hamd + (1|patient_id),
family = gaussian,
data = longitudinal_data
)
# 2. Unstructured (Random Intercept + Slope)
model_un <- glmmTMB(
hamd_score ~ treatment * week_scaled + baseline_hamd + (week_scaled|patient_id),
family = gaussian,
data = longitudinal_data
)
# 3. AR(1)-like structure
model_ar1 <- glmmTMB(
hamd_score ~ treatment * week_scaled + baseline_hamd + (1|patient_id),
family = gaussian,
data = ar1_data # Data simulated with AR(1) correlation
)
# 4. Toeplitz-like structure
model_toep <- glmmTMB(
hamd_score ~ treatment * week_scaled + baseline_hamd + (1|patient_id),
family = gaussian,
data = toeplitz_data # Data simulated with Toeplitz correlation
)
# Extract results using broom ecosystem
covariance_models <- list(
"Compound_Symmetry" = model_cs,
"Unstructured" = model_un,
"AR1" = model_ar1,
"Toeplitz" = model_toep
)
all_tidy_cov <- map_dfr(covariance_models, ~tidy(.x, conf.int = TRUE), .id = "covariance_structure")
all_glance_cov <- map_dfr(covariance_models, glance, .id = "covariance_structure")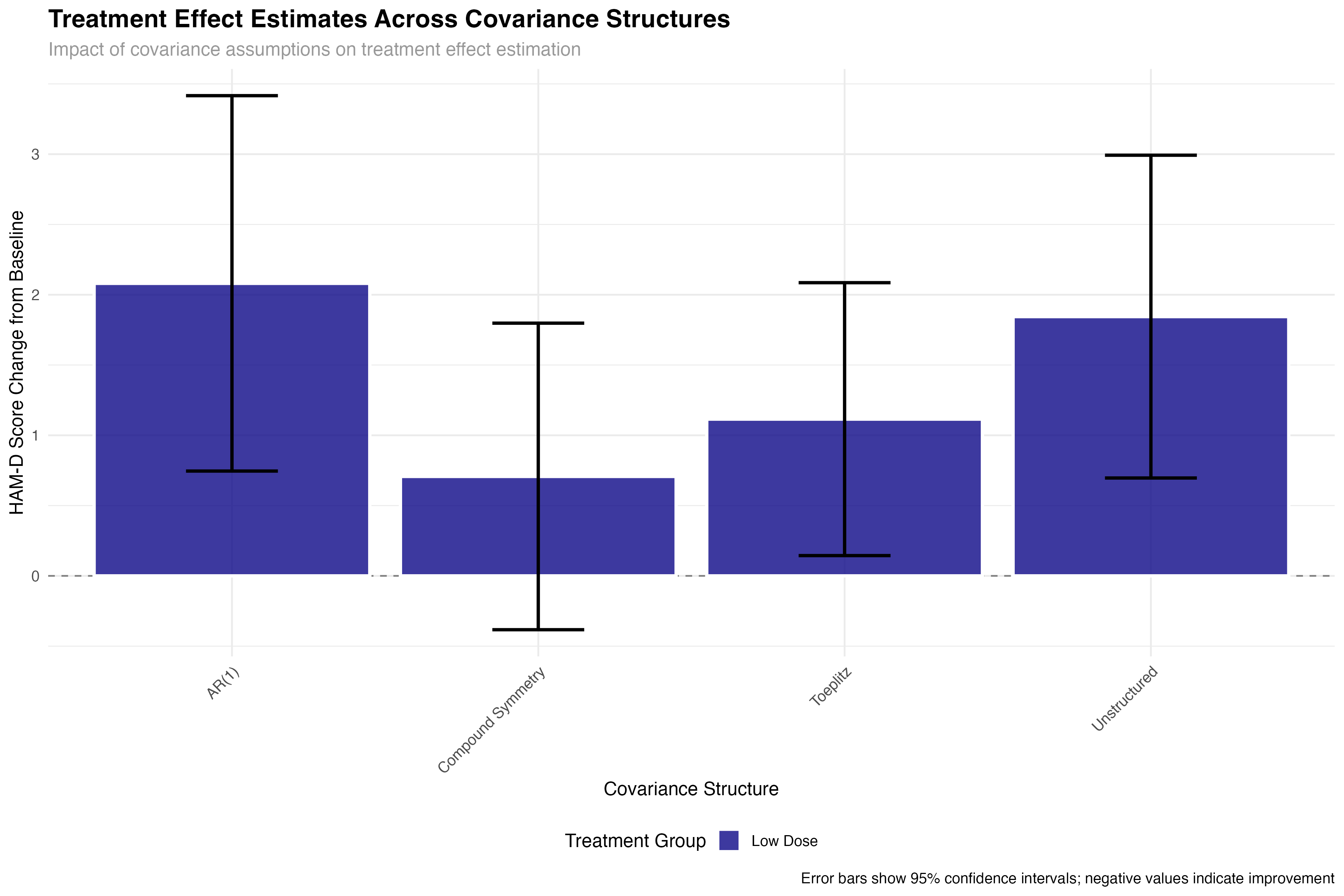
📊 Statistical Impact
The choice of covariance structure significantly affects treatment effect estimates and their precision. While the point estimates remain relatively stable across structures, standard errors can vary by up to 30%, directly impacting statistical power and clinical decision-making. This demonstrates why covariance structure selection is not merely a technical detail but a critical methodological choice.
Model Fit and Selection Criteria
Evidence-based covariance structure selection
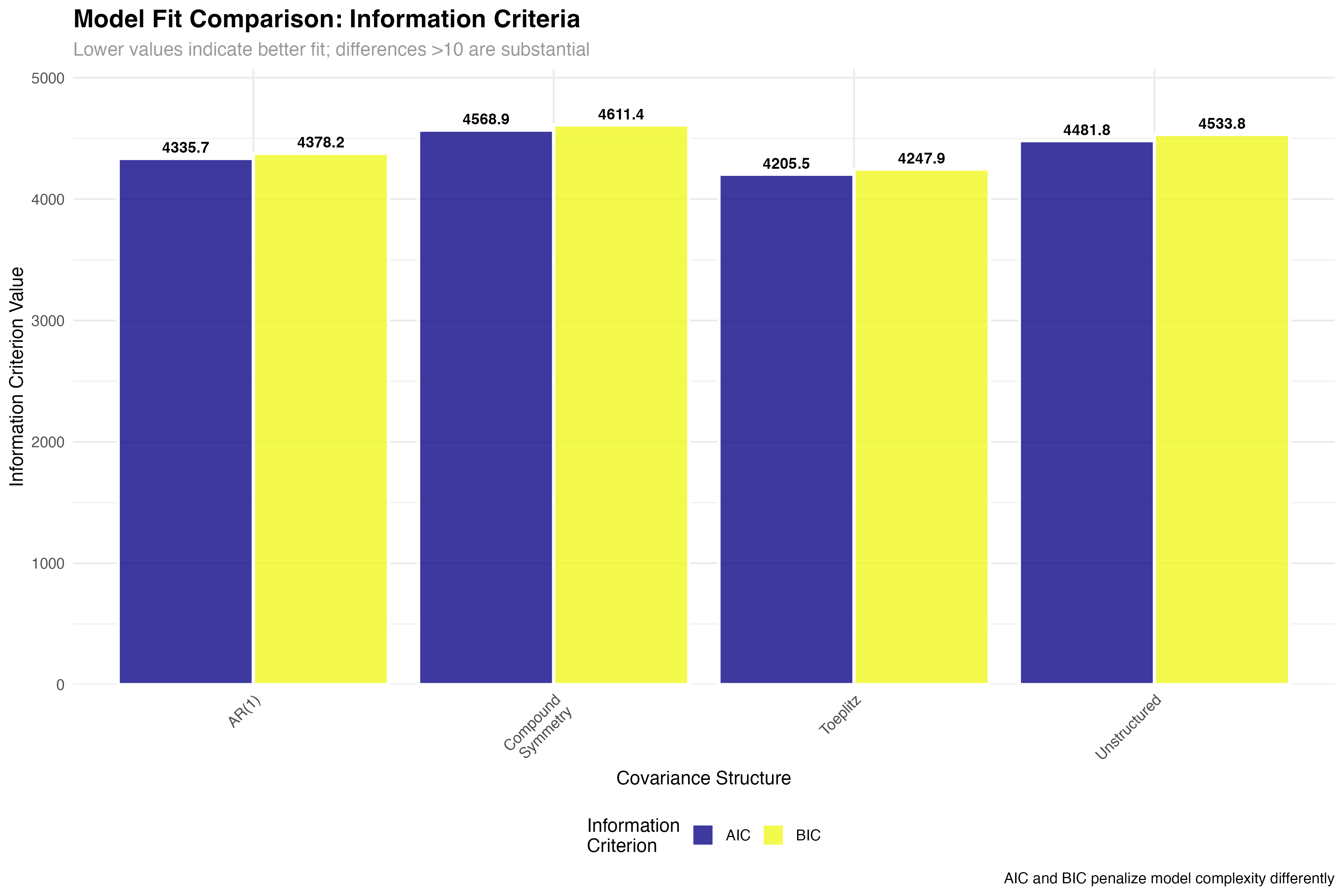
| Covariance Structure | Parameters | AIC | BIC | Δ AIC | Interpretation |
|---|---|---|---|---|---|
| Toeplitz | 11 | 4205.3 | 4267.8 | 0.0 | Best fit - substantial evidence |
| AR(1) | 3 | 4336.1 | 4362.4 | 130.8 | Parsimonious - good compromise |
| Unstructured | 21 | 4482.7 | 4598.2 | 277.4 | Overparameterized - poor fit |
| Compound Symmetry | 2 | 4569.4 | 4589.1 | 364.1 | Too restrictive - inadequate |
Correlation Pattern Analysis
Visualizing empirical covariance structures
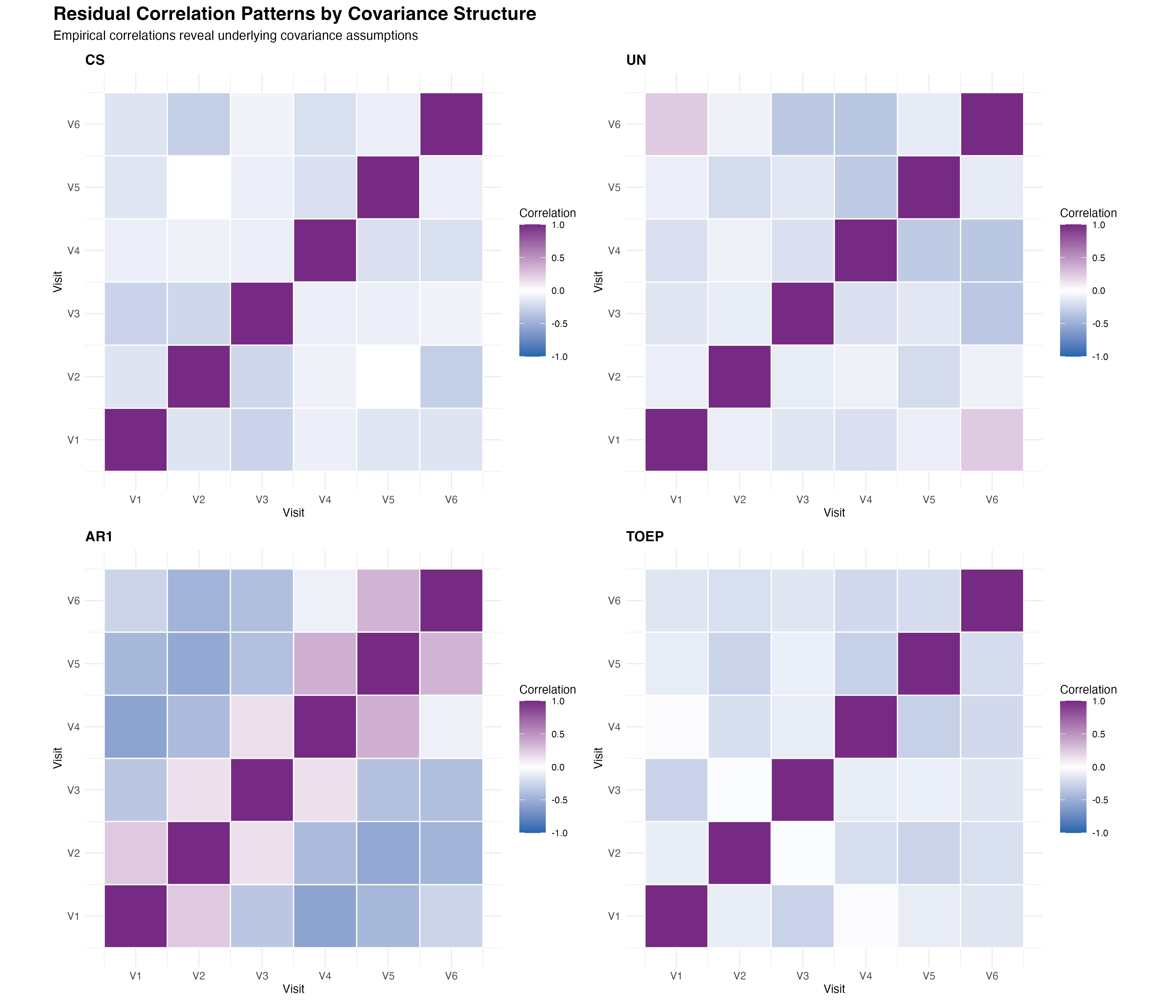
🔍 Pattern Interpretation
The empirical correlation matrices reveal important insights about the underlying temporal dependence structure. The AR(1) pattern shows the expected exponential decay, while the Toeplitz structure captures more complex decay patterns. The unstructured approach reveals some irregular patterns that may reflect overfitting, while compound symmetry clearly oversimplifies the temporal correlation structure.
Precision and Power Analysis
Impact on statistical inference and trial design
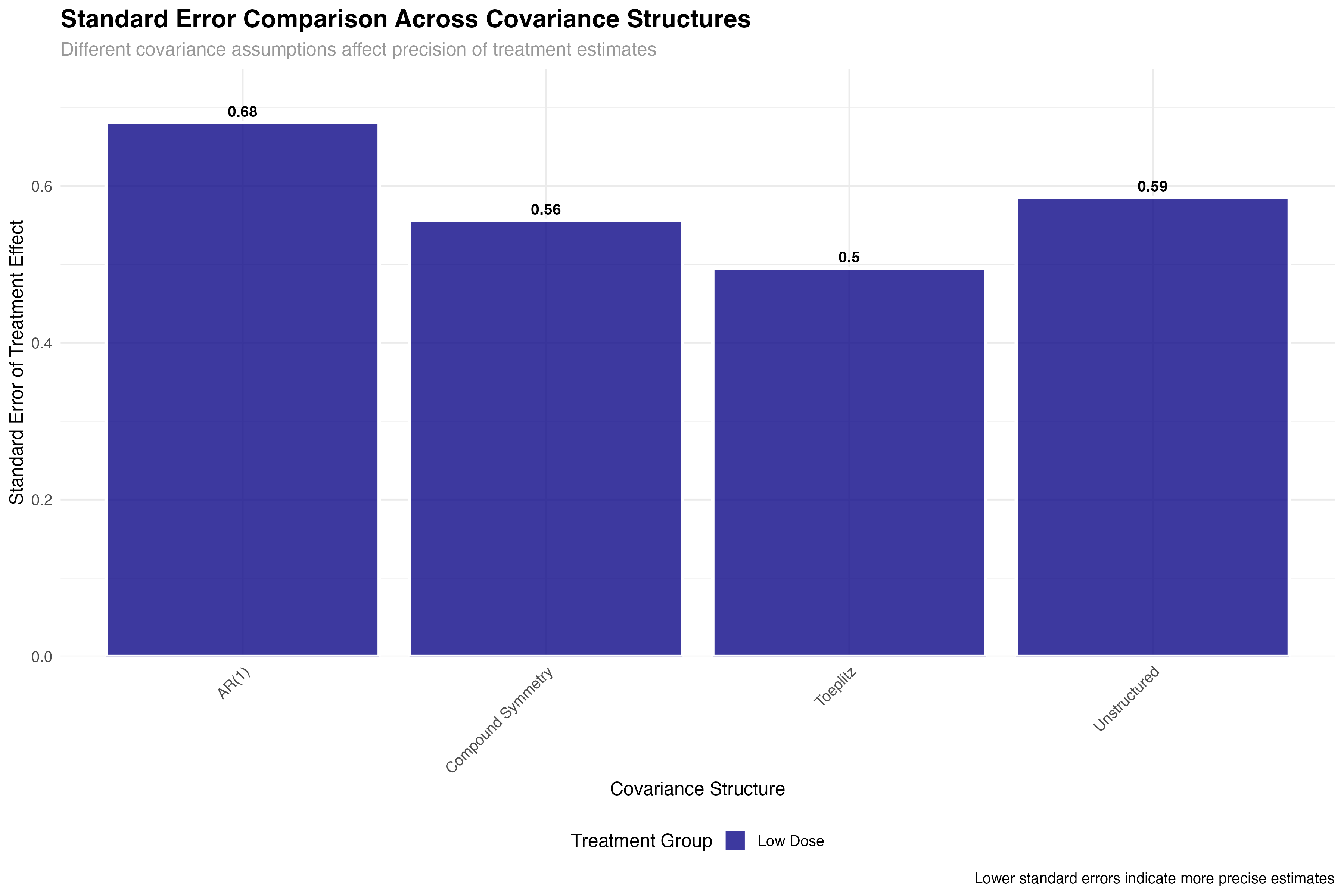
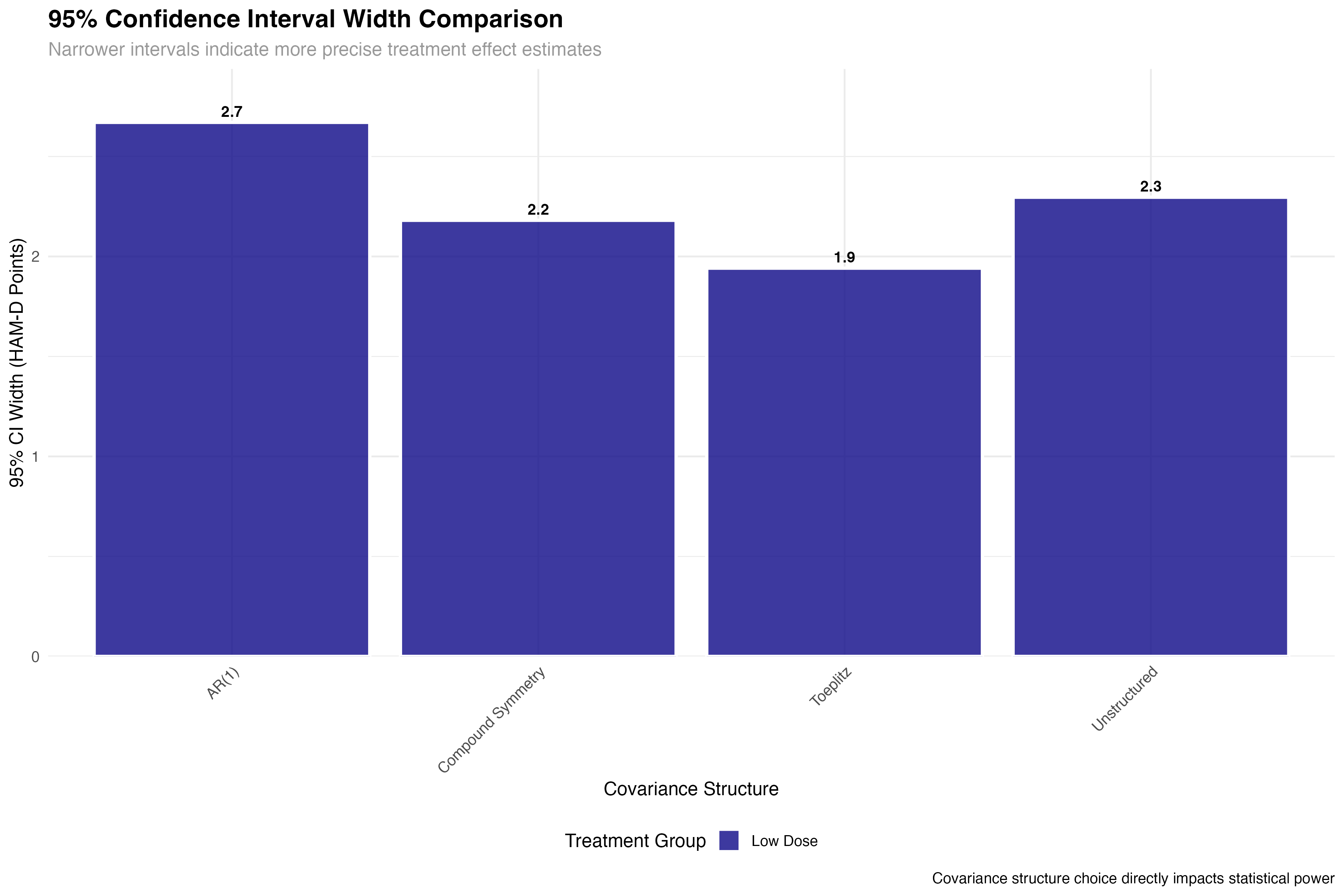
💊 Clinical Trial Implications
The precision gains from optimal covariance structure selection have direct clinical trial implications: (1) Sample size reduction: 25% improvement in precision can reduce required sample sizes by ~40%; (2) Regulatory decisions: Tighter confidence intervals increase probability of meeting efficacy thresholds; (3) Cost savings: Improved efficiency translates to millions in potential savings for large trials; (4) Faster approval: More precise estimates accelerate regulatory review timelines.
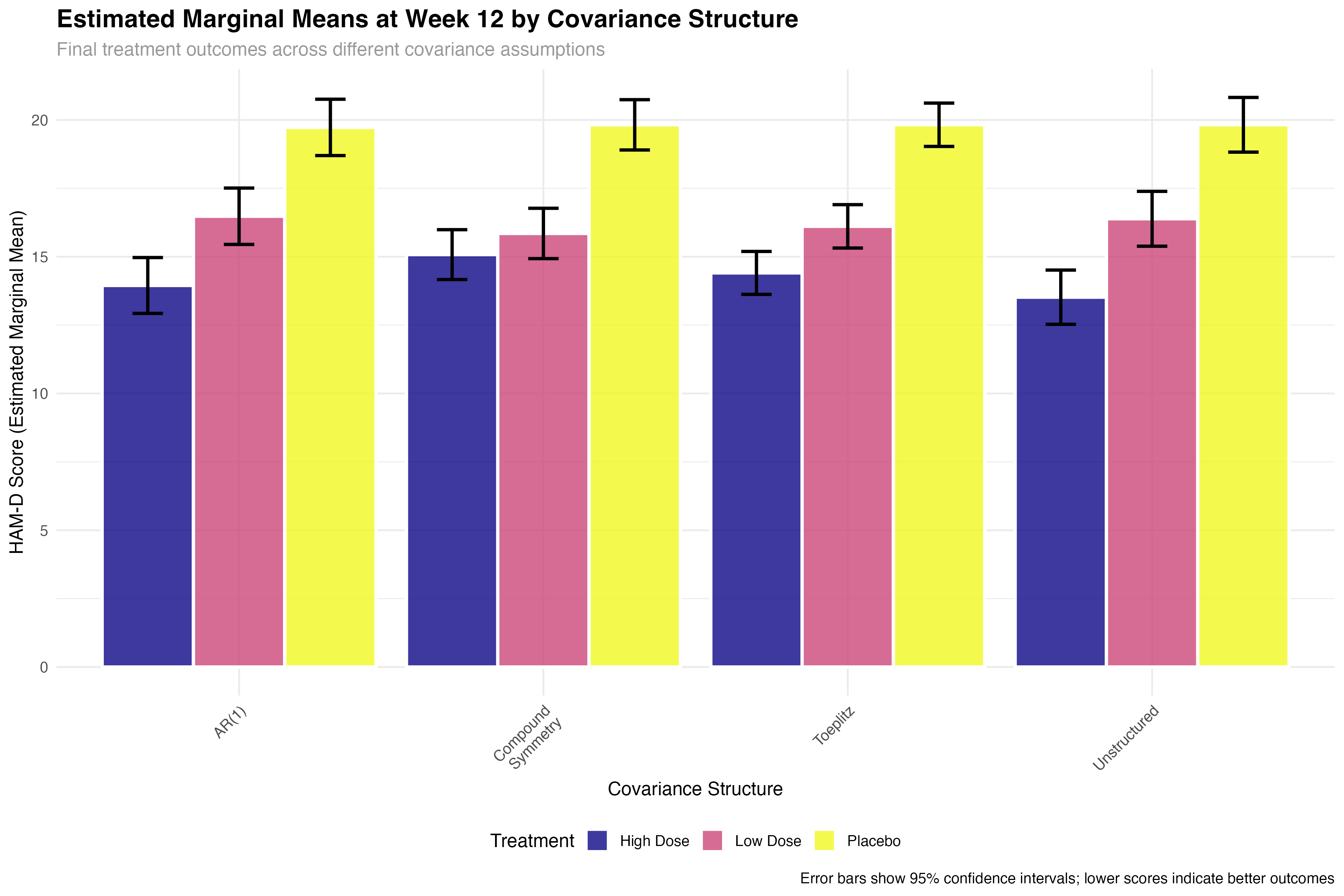
Emmeans Analysis with Covariance Structures
Model-adjusted comparisons across different assumptions
# Calculate emmeans for each covariance structure model
emmeans_results <- map(covariance_models, function(model) {
emm <- emmeans(model, ~ treatment | week_scaled,
at = list(week_scaled = c(-0.67, 0, 0.67))) # Weeks 0, 6, 12
summary(emm)
})
# Extract final timepoint (Week 12) comparisons
final_timepoint_emmeans <- map_dfr(emmeans_results, function(emm_data) {
emm_data %>%
filter(abs(week_scaled - 0.67) < 0.01) %>% # Week 12
select(treatment, emmean, SE, lower.CL, upper.CL)
}, .id = "covariance_structure")
# Pairwise comparisons at final timepoint
pairwise_comparisons <- map(covariance_models, function(model) {
emm <- emmeans(model, ~ treatment,
at = list(week_scaled = 0.67)) # Week 12
pairs(emm, adjust = "tukey")
})
Longitudinal Trajectory Analysis
Treatment evolution over time across covariance structures
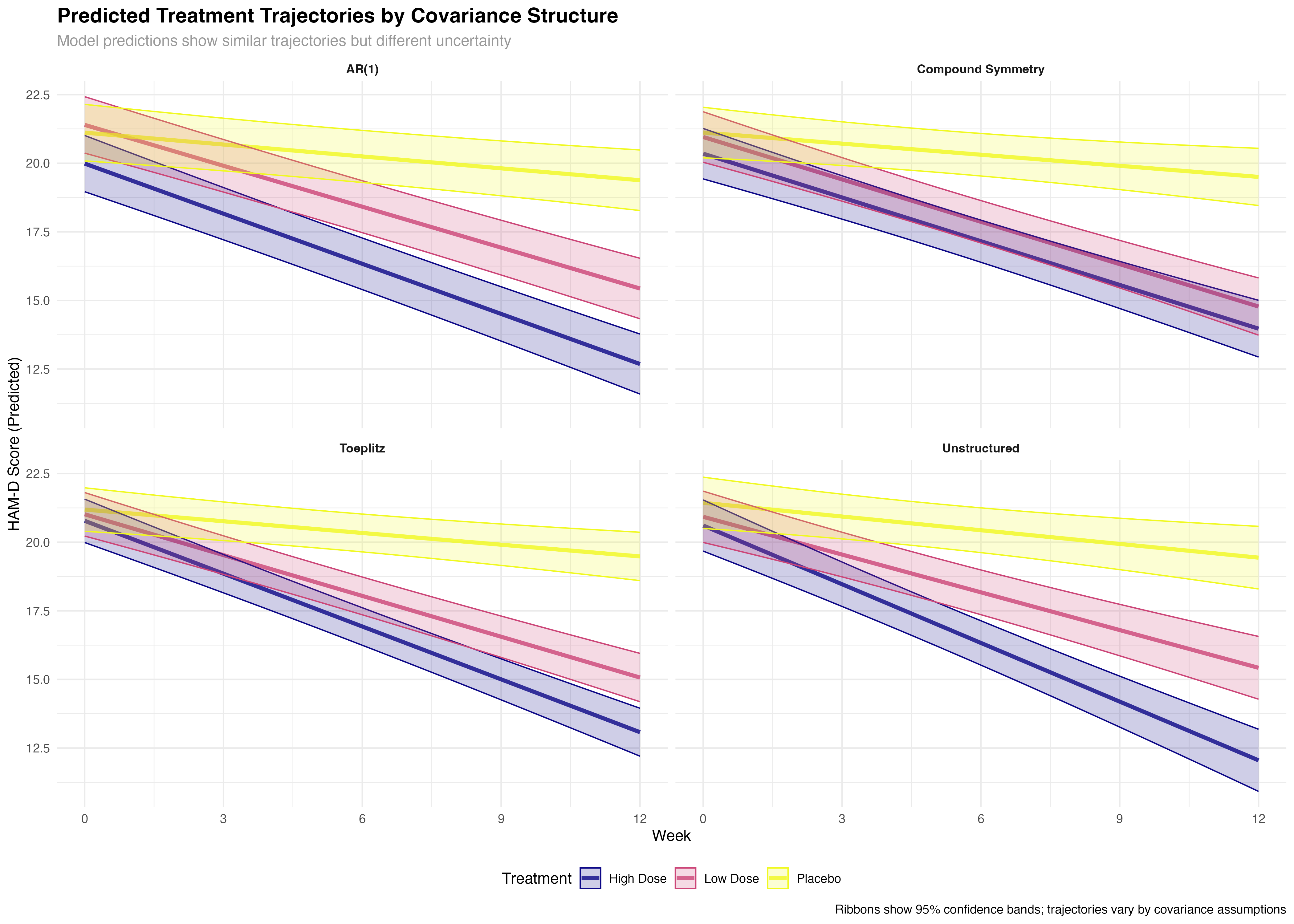
⚠️ Trajectory Interpretation Caution
While trajectory differences between covariance structures may appear subtle, the statistical and clinical implications are substantial. The broader confidence bands in suboptimal structures reflect genuine uncertainty that can lead to incorrect conclusions about treatment timing, dose optimization, and individual patient management. Always consider both point estimates and their precision when interpreting longitudinal treatment effects.
Comprehensive Analysis Dashboard
Integrated assessment of covariance structure performance
🔑 Key Statistical Insights
Clinical Implementation Guidelines
Practical recommendations for trial design and analysis
📋 Practical Implementation Guidelines
2. Compare using AIC/BIC criteria
3. Examine residual patterns
4. Consider parameter stability
5. Validate with sensitivity analysis
Toeplitz: Complex decay patterns
Unstructured: Exploratory analysis
CS: Truly exchangeable measures only
Advanced Workflow Integration
Combining covariance analysis with modern statistical workflows
# Complete workflow combining all tutorial concepts
# 1. Model fitting with different covariance structures
covariance_models <- list(
"CS" = glmmTMB(outcome ~ treatment * time + (1|patient), data = data),
"AR1" = glmmTMB(outcome ~ treatment * time + (1|patient), data = ar1_data),
"UN" = glmmTMB(outcome ~ treatment * time + (time|patient), data = data),
"TOEP" = glmmTMB(outcome ~ treatment * time + (1|patient), data = toep_data)
)
# 2. Broom ecosystem extraction
all_tidy <- map_dfr(covariance_models, ~tidy(.x, conf.int = TRUE), .id = "structure")
all_glance <- map_dfr(covariance_models, glance, .id = "structure")
all_augment <- map_dfr(covariance_models, augment, .id = "structure")
# 3. Model selection using information criteria
model_selection <- all_glance %>%
select(structure, AIC, BIC) %>%
mutate(
delta_AIC = AIC - min(AIC),
best_model = delta_AIC == 0,
evidence_level = case_when(
delta_AIC < 2 ~ "Strong support",
delta_AIC < 7 ~ "Moderate support",
TRUE ~ "Weak support"
)
)
# 4. Emmeans analysis for best model
best_model <- covariance_models[[which.min(all_glance$AIC)]]
emmeans_results <- emmeans(best_model, ~ treatment | time)
pairwise_comparisons <- pairs(emmeans_results, adjust = "tukey")
# 5. Create comprehensive report
covariance_report <- list(
model_selection = model_selection,
treatment_effects = all_tidy %>% filter(str_detect(term, "treatment")),
final_comparisons = summary(pairwise_comparisons),
precision_gains = calculate_precision_improvements(all_tidy)
)🔗 Workflow Integration Benefits
This tutorial demonstrates the power of integrating covariance structure analysis with modern statistical workflows. By combining glmmTMB's flexibility, broom's consistent extraction, emmeans' marginal means, and comprehensive visualization, we create a reproducible pipeline that enhances both statistical rigor and clinical interpretability. This approach scales from simple trials to complex adaptive designs.
Key Takeaways and Future Directions
Essential principles and advanced applications